Korrelationsfunktionen für die Bahnbewegungen von Doppelsternen
Click here for an English version
Hier gibt es das gepackte Postscript-File (diplom.zip, 2542703 Byte) zum Herunterladen.
In meiner Diplomarbeit habe ich mich mit einem recht neuen Gebiet der Astronomie, der Statistischen Astromerie, und hier genauer den mathematischen Methoden, die hinter dieser Theorie stehen, beschäftigt. Ziel dieser Arbeit war es, den Einfluß der Bahnbewegungen von Doppelsternen auf die durch Astrometrie-Satelliten wie HIPPARCOS immer genauer werdenden Positions- und Eigenbewegungsberechnungen zu bestimmen, um Fehler bei der statistischen Auswertung dieser Daten zu minimieren. Um einen etwas detaillierteren Einstieg in diese Thematik zu geben, habe ich hier die Einleitung aus meiner Diplomarbeit abgedruckt:
 Die statistische Astrometrie beschäftigt sich mit dem Einfluß nicht aufgelöster, astrometrischer Doppelsterne auf die High-Precision-Astrometrie. Unter Doppelsternen versteht man allgemein Systeme aus zwei oder mehr Sternen, die durch ihre gegenseitige gravitative Anziehung gebunden sind und deren Bahn um den gemeinsamen Schwerpunkt auf Ellipsen verläuft. Solche Systeme bilden den Großteil aller Sterne, während reine Einzelsterne nur einen kleinen Anteil an der Gesamtsternpopulation haben. Zur Vereinfachung werden im Rahmen dieser Arbeit nur Doppelsternsysteme bestehend aus zwei Sternen betrachtet. Als astrometrisch wird ein Doppelstern bezeichnet, wenn sein Photozentrum, d.h. Lichtschwerpunkt sich durch periodische Bahnveränderungen bemerkbar macht. Nebenstehend sind die wahre Bahn des Photozentrums eines Doppelsternsystems, die Tangentialebene am Himmel, in der man es beobachtet und einige Bahnelemente (Inklination i, Periastron und Knoten) dargestellt.
Die statistische Astrometrie beschäftigt sich mit dem Einfluß nicht aufgelöster, astrometrischer Doppelsterne auf die High-Precision-Astrometrie. Unter Doppelsternen versteht man allgemein Systeme aus zwei oder mehr Sternen, die durch ihre gegenseitige gravitative Anziehung gebunden sind und deren Bahn um den gemeinsamen Schwerpunkt auf Ellipsen verläuft. Solche Systeme bilden den Großteil aller Sterne, während reine Einzelsterne nur einen kleinen Anteil an der Gesamtsternpopulation haben. Zur Vereinfachung werden im Rahmen dieser Arbeit nur Doppelsternsysteme bestehend aus zwei Sternen betrachtet. Als astrometrisch wird ein Doppelstern bezeichnet, wenn sein Photozentrum, d.h. Lichtschwerpunkt sich durch periodische Bahnveränderungen bemerkbar macht. Nebenstehend sind die wahre Bahn des Photozentrums eines Doppelsternsystems, die Tangentialebene am Himmel, in der man es beobachtet und einige Bahnelemente (Inklination i, Periastron und Knoten) dargestellt.
Neben der Identifizierung von Sternen als Komponenten eines Doppelsternsystems durch astrometrische Methoden und damit Positionsbestimmungen gibt es visuelle, spektroskopische und photometrische Methoden. Visuelle Doppelsterne lassen sich mit Teleskopen trennen, man kann also in solchen Fällen die Komponenten des Systems direkt beobachten. Durch die Bewegung der Sterne um den Schwerpunkt nähern sich die Komponenten eines Doppelsterns auf einem Teil der Bahn im allgemeinen dem Beobachter, eine halbe Periode später dagegen entfernen sie sich von ihm. Ist die Bahn stark gegen den Beobachter geneigt, so ist dieser Effekt besonders groß. Solche Systeme machen sich durch den Dopplereffekt in Radialgeschwindigkeitsmessungen bemerkbar, man bezeichnet sie als spektroskopische Doppelsterne. Photometrische Doppelsterne schließlich sind Bedeckungsveränderliche. Bei diesen Systemen sieht man genau in die Bahnebene. Während des Umlaufs bedecken sich die beiden Komponenten gegenseitig, die Lichtkurven solcher Systeme nehmen dann ein Minimum an.
Verglichen mit der Zahl der beobachteten Sterne sind nur relativ wenige spektroskopische, photometrische, visuelle und astrometrische Doppelsterne bekannt. Mit zunehmender Genauigkeit moderner, astrometrischer Beobachtungsinstrumente steigt jedoch die Wahrscheinlichkeit, daß bisher nicht aufgelöste, astrometrische Doppelsterne einen im folgenden zu beschreibenden statistischen Einfluß auf die Genauigkeit der Messungen nehmen. Bisher war dieser Einfluß im wesentlichen vernachlässigbar, für HIPPARCOS und die geplante GAIA-Mission sind aber erhebliche Konsequenzen zu erwarten.
In der klassischen Astrometrie werden in der Regel alle Sterne als Einzelsterne angesehen, die mit konstanter Geschwindigkeit auf einer Geraden mit der Zeit fortschreiten. Doppelsterne werden in der Regel nicht betrachtet oder als seltene - da selten durch Messung bestätigte - Einzelfälle behandelt. Die Annahme einer linearen Bewegung ist aber selbst für Einzelsterne in Wirklichkeit nur in nullter Ordnung erfüllt, zusätzliche Effekte höherer Ordnung wie die der Realität näher kommende Bewegung des Sterns auf Großkreisen, die Berücksichtigung der sich ändernden Entfernung des Sterns von der Erde (foreshortening) durch deren jährliche Bewegung und die Änderung des Positionswinkels, der gegen die sich durch Präzession verlagernde Nordrichtung gemessen wird, müssen in realen Anwendungen berücksichtigt werden.
In Wirklichkeit sind aber, wie schon oben erwähnt, die meisten Sterne Komponenten eines Doppelsternsystems. Das Photozentrum solcher Systeme bewegt sich auf einer Ellipse um den Schwerpunkt. Es folgt damit nicht dem in der klassischen Astrometrie angenommenen linearen Bewegungsgesetz. Bei genügend hoher Meßgenauigkeit wird diese Abweichung von der CMS-Bewegung aber meßbar und das angenommene Modell wird für ein Ensemble von Sternen unzureichend. Auf diese Weise bringt die Orbitalbewegung des Photozentrums nicht aufgelöster, astrometrischer Doppelsterne eine statistische Komponente in die High-Precision-Astrometrie.
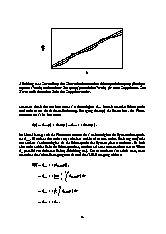
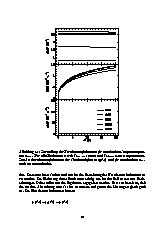
 Bemerkbar machen sich die Einschränkungen des linearen Modells, wenn man den Ort eines Photozentrums aus instantanen Messungen des Ortes und der Geschwindigkeit zur Epoche T für eine Epoche T+dt vorhersagen will. Durch die zusätzlich zur linearen Bewegung des Schwerpunktes auftretende, wellenförmige Bewegung des Photozentrums sind solchen Rechnungen auch im idealisierten Fall unendlich hoher Meßgenauigkeit Grenzen gesetzt. Signifikant wird die Abweichung zwischen linearem Modell und Beobachtung, wenn die Abweichung des beobachteten Ortes und der Geschwindigkeit von den entsprechenden Größen des physikalischen Schwerpunktes die Größenordnung der Meßfehler erreicht. Genaugenommen muß hier die Abweichung des Ortes von der mittleren Bewegung des Photozentrums, welche sich für stark elliptische Bahnen erheblich von der CMS-Bewegung unterscheidet, betrachtet werden. Dies ist in der nebenstehenden Abbildung zu sehen: Die durchgezogene Gerade entspricht der Bahn des Schwerpunktes, die gestrichelte der mittleren Bewegung des Photozentrums und die Kurve stellt die wahre Bahn des Photozentrums dar.
Bemerkbar machen sich die Einschränkungen des linearen Modells, wenn man den Ort eines Photozentrums aus instantanen Messungen des Ortes und der Geschwindigkeit zur Epoche T für eine Epoche T+dt vorhersagen will. Durch die zusätzlich zur linearen Bewegung des Schwerpunktes auftretende, wellenförmige Bewegung des Photozentrums sind solchen Rechnungen auch im idealisierten Fall unendlich hoher Meßgenauigkeit Grenzen gesetzt. Signifikant wird die Abweichung zwischen linearem Modell und Beobachtung, wenn die Abweichung des beobachteten Ortes und der Geschwindigkeit von den entsprechenden Größen des physikalischen Schwerpunktes die Größenordnung der Meßfehler erreicht. Genaugenommen muß hier die Abweichung des Ortes von der mittleren Bewegung des Photozentrums, welche sich für stark elliptische Bahnen erheblich von der CMS-Bewegung unterscheidet, betrachtet werden. Dies ist in der nebenstehenden Abbildung zu sehen: Die durchgezogene Gerade entspricht der Bahn des Schwerpunktes, die gestrichelte der mittleren Bewegung des Photozentrums und die Kurve stellt die wahre Bahn des Photozentrums dar.
Auch für die Geschwindigkeit ergibt sich ein statistischer Einfluß astrometrischer Doppelsterne. So stimmt die Geschwindigkeit im Gegensatz zu derjenigen bei linear angenommener Bewegung für zwei verschiedene Zeiten wegen der Orbitbewegung des Photozentrums im allgemeinen nicht überein; auch dieser Effekt wird meßbar, wenn die Abweichung der gemessenen Geschwindigkeit von der Schwerpunktgeschwindigkeit in die Größenordnung der Meßfehler gelangt.
Nicht nur bei der Vorhersage zukünftiger Örter und Geschwindigkeiten muß dem statistischen Einfluß astrometrischer Doppelsterne Rechnung getragen werden, auch die Fehlerrechnung muß modifiziert werden. Die Unsicherheit bei der Bestimmung z.B. des Ortes ergibt sich nicht mehr alleine aus den Meßfehlern, sondern man muß auch einen 'kosmischen Fehler' berücksichtigen. Dieser Begriff wurde erstmals von van den Kamp verwendet und von Wielen wieder aufgegriffen. Er beschreibt für ein Ensemble von Sternen die mittlere Abweichung von der gemittelten Orbitalbewegung und damit eine zusätzliche Unsicherheit in der Bestimmung des Ortes, da für das lineare Modell nur die mittlere Bewegung ausschlaggebend ist.
Will man bei der Bestimmung des zukünftigen Ortes aus den Messungen von Ort und Geschwindigkeit zu einer früheren Epoche den dabei gemachten Fehler abschätzen, so berechnet sich auch dieser nicht mehr alleine nach dem Gauß'schen Fehlerfortpflanzungsgesetz aus den Meßfehlern beider Beobachtungsgrößen (einschließlich der kosmischen Fehler), sondern es geht auch ein zweiter, zeitabhängiger kosmischer Fehler ein. Dieser ist klein, falls die Zeitdifferenz zwischen Beobachtung und Vorhersage klein ist, da dann das lineare Modell eine gute Approximation ist. Für große Zeiten dagegen dominiert der zeitabhängige kosmische Fehler.
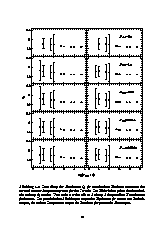
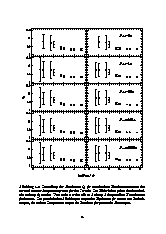
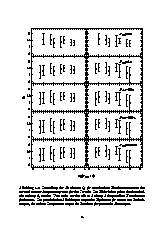
In dieser Arbeit sollen die oben beschriebenen statistischen Einflüsse nicht aufgelöster, astrometrischer Doppelsterne auf die High-Precision-Astrometrie qualitativ und quantitativ untersucht werden. Eine besonders elegante Formulierung der statistischen Astrometrie ist mit Hilfe von Korrelationsfunktionen für die Bahnbewegungen von Doppelsternen möglich. Ein Ziel dieser Arbeit ist es, diese Funktionen eingehend zu untersuchen. Zudem werden Anwendungen der Korrelationsfunktionen in der statistischen Astrometrie aufgezeigt.
Wer mag, kann sich die einzelnen Seiten auch im Internet ansehen, ich habe sie nach Kapiteln angeordnet. Die einzelnen Seiten sind als Thumbnails dargestellt, durch Anklicken bekommt man die vergrößerte Version. Wenn das Laden der Thumbnails zu lange dauert, kann man auch auf sie verzichten; in diesem Fall sollte man hier klicken.




Zusammenfassung


Inhaltsverzeichnis


Kapitel I: Einleitung



Kapitel II: Grundlagen





































Kapitel III: Ein einfaches Beispiel: Kreisbahnen







Kapitel IV: Elliptische Doppelsternbahnen















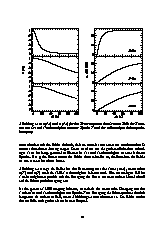
Anhang A: Korrelationsfunktionen

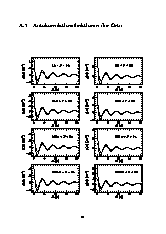


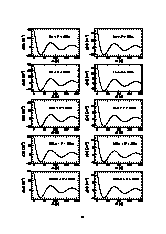
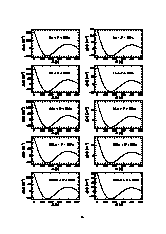
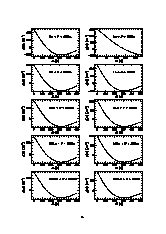

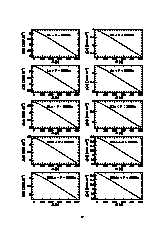

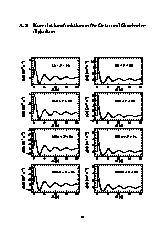

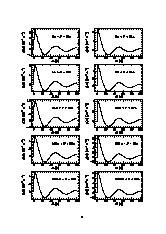




Anhang B: Korrelationsfunktionen für eingescchränkte Ensembles







Literaturverzeichnis




Danksagung


Erklärung


Zurück zur Homepage
Letzte Änderung: 29.03.2000

webmaster@michael-biermann.de
 Die statistische Astrometrie beschäftigt sich mit dem Einfluß nicht aufgelöster, astrometrischer Doppelsterne auf die High-Precision-Astrometrie. Unter Doppelsternen versteht man allgemein Systeme aus zwei oder mehr Sternen, die durch ihre gegenseitige gravitative Anziehung gebunden sind und deren Bahn um den gemeinsamen Schwerpunkt auf Ellipsen verläuft. Solche Systeme bilden den Großteil aller Sterne, während reine Einzelsterne nur einen kleinen Anteil an der Gesamtsternpopulation haben. Zur Vereinfachung werden im Rahmen dieser Arbeit nur Doppelsternsysteme bestehend aus zwei Sternen betrachtet. Als astrometrisch wird ein Doppelstern bezeichnet, wenn sein Photozentrum, d.h. Lichtschwerpunkt sich durch periodische Bahnveränderungen bemerkbar macht. Nebenstehend sind die wahre Bahn des Photozentrums eines Doppelsternsystems, die Tangentialebene am Himmel, in der man es beobachtet und einige Bahnelemente (Inklination i, Periastron und Knoten) dargestellt.
Die statistische Astrometrie beschäftigt sich mit dem Einfluß nicht aufgelöster, astrometrischer Doppelsterne auf die High-Precision-Astrometrie. Unter Doppelsternen versteht man allgemein Systeme aus zwei oder mehr Sternen, die durch ihre gegenseitige gravitative Anziehung gebunden sind und deren Bahn um den gemeinsamen Schwerpunkt auf Ellipsen verläuft. Solche Systeme bilden den Großteil aller Sterne, während reine Einzelsterne nur einen kleinen Anteil an der Gesamtsternpopulation haben. Zur Vereinfachung werden im Rahmen dieser Arbeit nur Doppelsternsysteme bestehend aus zwei Sternen betrachtet. Als astrometrisch wird ein Doppelstern bezeichnet, wenn sein Photozentrum, d.h. Lichtschwerpunkt sich durch periodische Bahnveränderungen bemerkbar macht. Nebenstehend sind die wahre Bahn des Photozentrums eines Doppelsternsystems, die Tangentialebene am Himmel, in der man es beobachtet und einige Bahnelemente (Inklination i, Periastron und Knoten) dargestellt.
 Bemerkbar machen sich die Einschränkungen des linearen Modells, wenn man den Ort eines Photozentrums aus instantanen Messungen des Ortes und der Geschwindigkeit zur Epoche T für eine Epoche T+dt vorhersagen will. Durch die zusätzlich zur linearen Bewegung des Schwerpunktes auftretende, wellenförmige Bewegung des Photozentrums sind solchen Rechnungen auch im idealisierten Fall unendlich hoher Meßgenauigkeit Grenzen gesetzt. Signifikant wird die Abweichung zwischen linearem Modell und Beobachtung, wenn die Abweichung des beobachteten Ortes und der Geschwindigkeit von den entsprechenden Größen des physikalischen Schwerpunktes die Größenordnung der Meßfehler erreicht. Genaugenommen muß hier die Abweichung des Ortes von der mittleren Bewegung des Photozentrums, welche sich für stark elliptische Bahnen erheblich von der CMS-Bewegung unterscheidet, betrachtet werden. Dies ist in der nebenstehenden Abbildung zu sehen: Die durchgezogene Gerade entspricht der Bahn des Schwerpunktes, die gestrichelte der mittleren Bewegung des Photozentrums und die Kurve stellt die wahre Bahn des Photozentrums dar.
Bemerkbar machen sich die Einschränkungen des linearen Modells, wenn man den Ort eines Photozentrums aus instantanen Messungen des Ortes und der Geschwindigkeit zur Epoche T für eine Epoche T+dt vorhersagen will. Durch die zusätzlich zur linearen Bewegung des Schwerpunktes auftretende, wellenförmige Bewegung des Photozentrums sind solchen Rechnungen auch im idealisierten Fall unendlich hoher Meßgenauigkeit Grenzen gesetzt. Signifikant wird die Abweichung zwischen linearem Modell und Beobachtung, wenn die Abweichung des beobachteten Ortes und der Geschwindigkeit von den entsprechenden Größen des physikalischen Schwerpunktes die Größenordnung der Meßfehler erreicht. Genaugenommen muß hier die Abweichung des Ortes von der mittleren Bewegung des Photozentrums, welche sich für stark elliptische Bahnen erheblich von der CMS-Bewegung unterscheidet, betrachtet werden. Dies ist in der nebenstehenden Abbildung zu sehen: Die durchgezogene Gerade entspricht der Bahn des Schwerpunktes, die gestrichelte der mittleren Bewegung des Photozentrums und die Kurve stellt die wahre Bahn des Photozentrums dar.